by R. Grothmann
Gauss integration is defined in Euler in the gauss() function. We like to show, how to derive a Gauss formula.
First we need the Legendre polynomials. These polynomials are orthogonal on [-1,1]. We simply use Gram-Schmidt. To ease the compuation, we define the scalar product in Maxima.
>function sp(f,g) &&= integrate(f*g,x,-1,1)
integrate(f g, x, - 1, 1)
Then we need p0 to p4.
>p0 &= 1; >p1 &= x; >p2 &= x^2-sp(x^2,p0)/sp(p0,p0)*p0
2 1
x - -
3
>p3 &= x^3-sp(x^3,p1)/sp(p1,p1)*p1
3 3 x
x - ---
5
>p4 &= x^4-sp(x^4,p2)/sp(p2,p2)*p2-sp(x^4,p0)/sp(p0,p0)*p0 | ratsimp
4 2
35 x - 30 x + 3
-----------------
35
There is a function legendre(), which computes these polynomials using a recursion formula.
>fracprint(legendre(4)*8)
[3, 0, -30, 0, 35]
This agrees with the result of Maxima.
>&expand(legendre_p(4,x)*8)
4 2
35 x - 30 x + 3
We need the zeros of p4. Maxima can provide these zeros in exact form.
>&solve(p4), xnode=%()
sqrt(2 sqrt(30) + 15) sqrt(2 sqrt(30) + 15)
[x = - ---------------------, x = ---------------------,
sqrt(35) sqrt(35)
sqrt(15 - 2 sqrt(30)) sqrt(15 - 2 sqrt(30))
x = - ---------------------, x = ---------------------]
sqrt(35) sqrt(35)
[-0.861136, 0.861136, -0.339981, 0.339981]
Now we need to define the coefficients of the formula. We solve the equation
![]()
for
![]()
The matrix language of Euler lets us easily define a linear system for this.
>A=xnode^((0:3)'); b=(2*[1,0,1/3,0])'; ... alpha=(A\b)'
[0.347855, 0.347855, 0.652145, 0.652145]
These values can also be obtained by the Christoffel function in the following way.
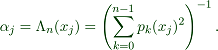
For this, the polynomials must be normalized with respect to the L2-norm.
>function C4(x) &= 1/sum(legendre_p(n,x)^2/ ... integrate(legendre_p(n,x)^2,x,-1,1),n,0,3) | ratsimp
8
---------------------------
6 4 2
175 x - 165 x + 45 x + 9
Indeed, we get exactly the same values.
>C4(xnode)
[0.347855, 0.347855, 0.652145, 0.652145]
We can test this for the interval [-1,1].
>function map gauss5test (f) := sum(f(xnode)*alpha); ... fraction gauss5test(["1","x","x^2","x^3","x^4","x^5","x^6","x^7","x^8"])
[2, 0, 2/3, 0, 2/5, 0, 2/7, 0, 258/1225]
The result is exact for polynomials of degree 7.
We define a function for this integration using the Euler matrix language. The matrix X in the following function, contains all knots in all subintervals. Knots with equal coefficients are collected in each row.
>function gauss5test (f,a:number,b:number,n=1,xn=xnode,al=alpha) ... h=(b-a)/n; if n>1 then x=linspace(a+h/2,b-h/2,n-1); else x=a+h/2; endif; X=x-(h/2*xn)'; return sum(al.f(X))*h/2 endfunction
Test.
>fracprint(gauss5test("x^6",0,1))
1/7
Let us test some more functions. The n=10 subintervals are 40 function evaluations.
>longestformat; gauss5test("exp(x)",0,1,10)-(E-1)
4.440892098500626e-016
The function is already defined in Euler.
>longestformat; gauss5("exp(x)",0,1,10)-(E-1)
4.440892098500626e-016
Note that
![]()
The Simpson method is not so good, but takes half as many function evaluations.
>simpson("exp(x)",0,1,10)-(E-1)
5.964481175624314e-008
The Gauss algorithm with 10 knots gets the same result with only 10 evaluations.
>gauss("exp(x)",0,1)-(E-1)
2.220446049250313e-016
Here is a test with the Gauss distribution.
>gauss5("exp(-x^2/2)",0,10,n=10)/sqrt(2*pi)
0.5000000000028569
>gauss("exp(-x^2/2)",0,10,n=10)/sqrt(2*pi)
0.5000000000000001
In the following, we compute the Legendre polynimals explicitely using the symbolic functions of Euler and Maxima.
The Legendre satisfy the following recursion formula.
![]()
To program such a recursion in Maxima, we define the following purely symbolic function with a function body containing a block of statements.
>function L(x,n) &&= block ( ... if n=0 then 1 ... else if n=1 then x ... else ((2*n-1)*x*L(x,n-1)-(n-1)*L(x,n-2))/n )
block(if n = 0 then 1 else (if n = 1 then x
(2 n - 1) x L(x, n - 1) - (n - 1) L(x, n - 2)
else ---------------------------------------------))
n
>&L(x,2)
2
3 x - 1
--------
2
Let us check the orthogonality.
>&integrate(L(x,2)*L(x,1),x,-1,1)
0
>&integrate(L(x,2)*L(x,0),x,-1,1)
0
>&integrate(L(x,3)*L(x,2),x,-1,1)
0
The norm of L(x,n) is 2/(2n+1).
>&integrate(L(x,2)*L(x,2),x,-1,1)
2
-
5
The Legendre polynomials satisfy the following differential equation.
>eq &= -2*x*'diff(y,x)+(1-x^2)*'diff(y,x,2)+n*(n+1)*y=0
2
2 d y dy
(1 - x ) --- - 2 x -- + n (n + 1) y = 0
2 dx
dx
Test for n=3
>& eq | [n=3,y=L(x,3)], & % | nouns | ratsimp
2
5 x (3 x - 1)
2 -------------- - 2 x
2 d 2
(1 - x ) (--- (--------------------))
2 3
dx
2
5 x (3 x - 1)
-------------- - 2 x 2
d 2 5 x (3 x - 1)
- 2 x (-- (--------------------)) + 4 (-------------- - 2 x) = 0
dx 3 2
0 = 0
The main Maxima command ode2 cannot solve this.
>& eq | n=2, &ode2(%,y,x)
2
2 d y dy
(1 - x ) --- - 2 x -- + 6 y = 0
2 dx
dx
false
The two term recursive definition can get ineffective. So we replace it with a loop.
>function L(x,n) &&= block( if n=0 then 1 else block([y:[1,x]], ... for i:2 thru n do y:[y[2],expand(((2*i-1)*x*y[2]-(i-1)*y[1])/i)], y[2]));
Test.
>& L(x,2) | ratsimp
2
3 x - 1
--------
2
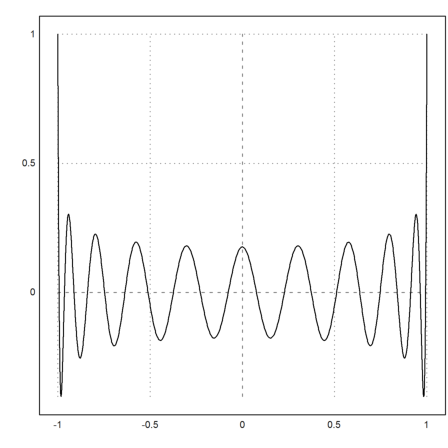
We can now use polynomials of high degree.
>plot2d(& L(x,20) | expand,-1,1):
For other weights, we could do just the same.
>function sp(f,g) &&= integrate(f*g*exp(-x),x,-1,1)
- x
integrate(f g E , x, - 1, 1)
Then we need p0 to p4.
>p0 &= 1; >p1 &= x-sp(x,p0)/sp(p0,p0)|ratsimp
2
(E - 1) x + 2
--------------
2
E - 1
>p2 &= x^2-sp(x^2,p1)/sp(p1,p1)*p1-sp(x^2,p0)/sp(p0,p0)*p0|ratsimp
4 2 2 4 2 4 2
(E - 6 E + 1) x + (- 2 E + 16 E - 6) x - E + 6 E + 7
-----------------------------------------------------------
4 2
E - 6 E + 1
If we continue like this, we get fairly complicated polynomials. We like to demonstrate, how to use numerical integration instead.
First, we define the function to integrate.
>function p(x,i) := x^i*exp(-x)
Then the integral.
>function map a(i) := gauss("p",-1,1,100;i)
A test.
>a(5)
-0.3242973696922066
>&integrate(x^5*exp(-x),x,-1,1), %()
- 1
44 E - 326 E
-0.3242973696922178
It becomes obvious, that the result is not perfect. We either have to live with this, or to derive and use a recursion formula, or the exact symbolic method.
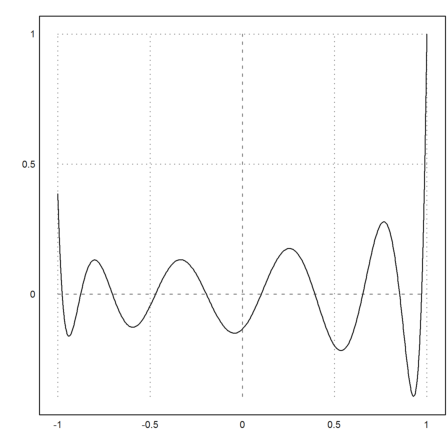
We need the 10-th orthogonal polynomial. To compute it, we use the Gram matrix.
>A=a((0:10)+(0:9)')_1; b=zeros(10,1)_1; >p=xlgs(A,b)';
Here is a plot of this polynomial.
>plot2d("polyval(p,x)",-1,1):
Let us test the orthogonality.
>for i=0 to 9; gauss("x^i*polyval(p,x)*exp(-x)",-1,1,100), end;
1.23084875625068e-014 -7.745415420146173e-014 -1.233568802661011e-014 3.418543226274551e-014 3.103073353827313e-016 -2.974398505273257e-014 -1.885935851930754e-014 6.401379426534959e-014 3.972544515562504e-014 -5.778488798569015e-014
Next we need the zeros.
>xn=sort(real(polysolve(p)))
[-0.9761983950159177, -0.876341759205208, -0.7038368925296208, -0.4708613994245012, -0.1948808338591103, 0.1018814014714706, 0.3935411401555917, 0.6524949822560991, 0.8523013113814679, 0.9712722677116907]
Then we need the coefficients, which make the integration exact for polynomials up to degree 9.
>M=xn^((0:9)'); b=a((0:9)'); >al=xlgs(M,b)'
[0.1616042035976784, 0.3308952772834531, 0.4148551396265188, 0.4128502394503031, 0.3529200553213233, 0.2698111100739772, 0.1888527845927684, 0.1216033541103824, 0.06925902427714205, 0.02775119895405546]
We can use the same code as above to define the Gauss integrator.
>function gauss10exp (f,a:number,b:number,n=1,xn=xn,al=al) ... h=(b-a)/n; if n>1 then x=linspace(a+h/2,b-h/2,n-1); else x=a+h/2; endif; X=x-(h/2*xn)'; return sum(al.f(X))*h/2 endfunction
Let us test with the integral of cos(x)*exp(-x).
>gauss10exp("cos(x)",-1,1)
1.933421496200713
This is the Gauß formula for one sub-interval.
>sum(cos(xn)*al)
1.933421496200713
The result is absolutely exact to all digits.
>&integrate(cos(x)*exp(-x),x,-1,1); %()
1.933421496200713